
If we wanted to be really specific when naming our triangles, we can combine names from each group one from the first group and one from the second group.įor instance, the triangle above is an acute scalene triangle. So far, we’ve covered six types of triangles, which is technically all of the types, but we’re not done yet. And when none of the angles are the same it’s a scalene triangle. When two of the angles are the same it’s an isosceles triangle. Technically, it’s called an equiangular triangle but they’re exactly the same thing because all equilateral triangles are also equiangular triangles. When all the angles are the same 60 degrees, it’s an equilateral triangle.
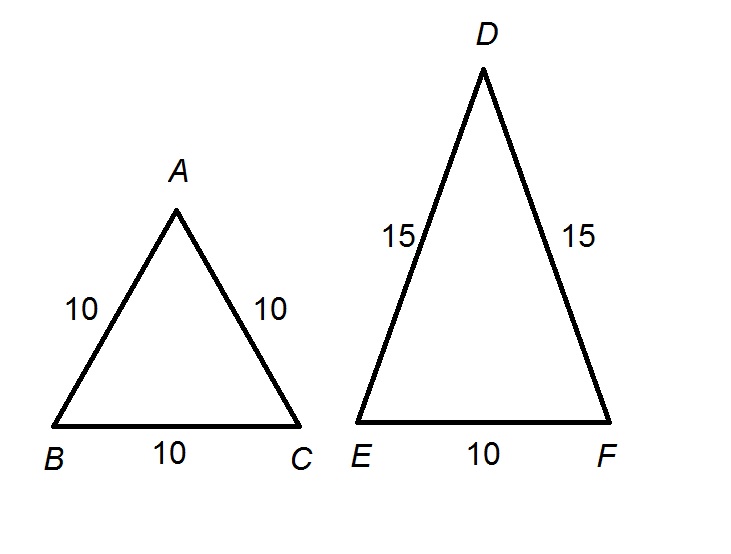
While you often see these three types of triangles identified by the lengths of their sides, they can also be categorized by their angles. In our last triangle, none of the sides have the same length, so this is called a scalene triangle. It’s a hard one to spell, but an easy one to recognize! Scalene Triangle When two of the sides of a triangle are the same it’s called an isosceles triangle. In the middle triangle, we can see that two of the sides are the same length and measure 8 cm while the third is 9 cm. It’s not too tough of a name to remember since the beginning of equilateral sounds like the word equal, and the word lateral means “side.” Isosceles Triangle A triangle like this one where all the sides are the same is called an equilateral triangle. In the triangle on the left, we can see that all three sides are the same length and measure 9 centimeters. Here are three triangles with the lengths of the sides included: Our second set of triangles is categorized by how many of the sides have the same length. That’s all there is to it for these three types! We just find the largest angle and the name of the triangle will correspond to the name of that angle. Because this is more than 90 degrees, this is an obtuse angle, so we call this triangle an obtuse triangle. Obtuse Triangleįinally, in the triangle on the right, the largest angle is 117 degrees. You might remember that a 90-degree angle is a right angle, so this triangle is a right triangle. We can see that in the middle triangle the largest angle is exactly 90 degrees. This one is easy to remember, since “cute” things are often small, like puppies and kittens. Just remember that acute angles are less than 90 degrees. 70 is less than 90, so this is an acute triangle. We can see that the largest angle in the triangle on the left is 70 degrees. These are the acute, right, and obtuse triangles.īut how do you know which is which? Take a look at the largest angle of each triangle and note whether or not the angle is more than, less than, or equal to 90 degrees. Let’s start with the three types of triangles that are categorized by the measure of their largest angle. We’re going to break our six types of triangles into two groups of three. This is true for all triangles, including the six types we’re looking at today. In addition, a triangle has three interior angles, and the sum of those three angles is always 180 degrees. The length of the sides can vary but the length of the largest side can’t be equal or greater to the sum of the other two sides. The two angles opposite the legs are equal and are always acute, so the classification of the triangle as acute, right, or obtuse depends only on the angle between its two legs.Hi, and welcome to this review of different types of triangles! Before we begin, here’s a review of the basics.Ī triangle has three straight sides that connect. The other dimensions of the triangle, such as its height, area, and perimeter, can be calculated by simple formulas from the lengths of the legs and base.Įvery isosceles triangle has an axis of symmetry along the perpendicular bisector of its base.

The two equal sides are called the legs and the third side is called the base of the triangle. Isosceles triangles have been used as decoration from even earlier times, and appear frequently in architecture and design, for instance in the pediments and gables of buildings. The mathematical study of isosceles triangles dates back to ancient Egyptian mathematics and Babylonian mathematics.
Isosceles triangle with vertical axis of symmetry


 0 kommentar(er)
0 kommentar(er)
